Lumière
Les Notions et Attendus
- Source, propagation, vitesse de propagation
- Modèle du rayon lumineux
- Savoir que la matière peut émettre de la lumière
- Savoir comment la matière interagit avec la lumière
- Citer la valeur de la vitesse de la lumière dans le vide ou dans l’air et la comparer à d’autres valeurs de vitesses couramment rencontrées.
- Expliquer l'influence de l'indice optique d’un milieu matériel sur la lumière.
- Connaître et exploiter les lois de Snell-Descartes pour la réflexion et la réfraction.
- Caractériser les foyers d’une lentille mince convergente à l’aide du modèle du rayon lumineux.
- Utiliser le modèle du rayon lumineux pour déterminer graphiquement la position, la taille et le sens de l’image réelle d’un objet plan réel donnée par une lentille mince convergente.
- Définir et déterminer géométriquement un grandissement.
- Modéliser l’œil et expliquer qualitativement comment il forme l'image d'un objet
- Décrire et expliquer qualitativement le phénomène de dispersion de la lumière par un prisme.
- Caractériser un rayonnement monochromatique par sa longueur d’onde dans le vide ou dans l’air.
- Caractériser le spectre d'émission du rayonnement émis par un corps chaud.
- Exploiter un spectre de raies.
- Tester les lois de Snell-Descartes à partir d’une série de mesures et déterminer l’indice de réfraction d’un milieu.
- Produire et exploiter des spectres d’émission obtenus à l’aide d’un système dispersif et d’un analyseur de spectre.
- Produire et caractériser l’image réelle d’un objet plan réel formée par une lentille mince convergente.
Le cours
1. Emission et Interaction avec la matière
Emission par un corps chaud
Si on chauffe suffisamment la matière, elle peut émettre de la lumière visible. C'est le principe de fonctionnement de la lampe à incandescence.Interaction
La matière est capable de réfléchir, absorber et transmettre la lumière qu'elle reçoit. La lumière absorbée est convertie en un autre type d'énergie (énergie thermique par exemple).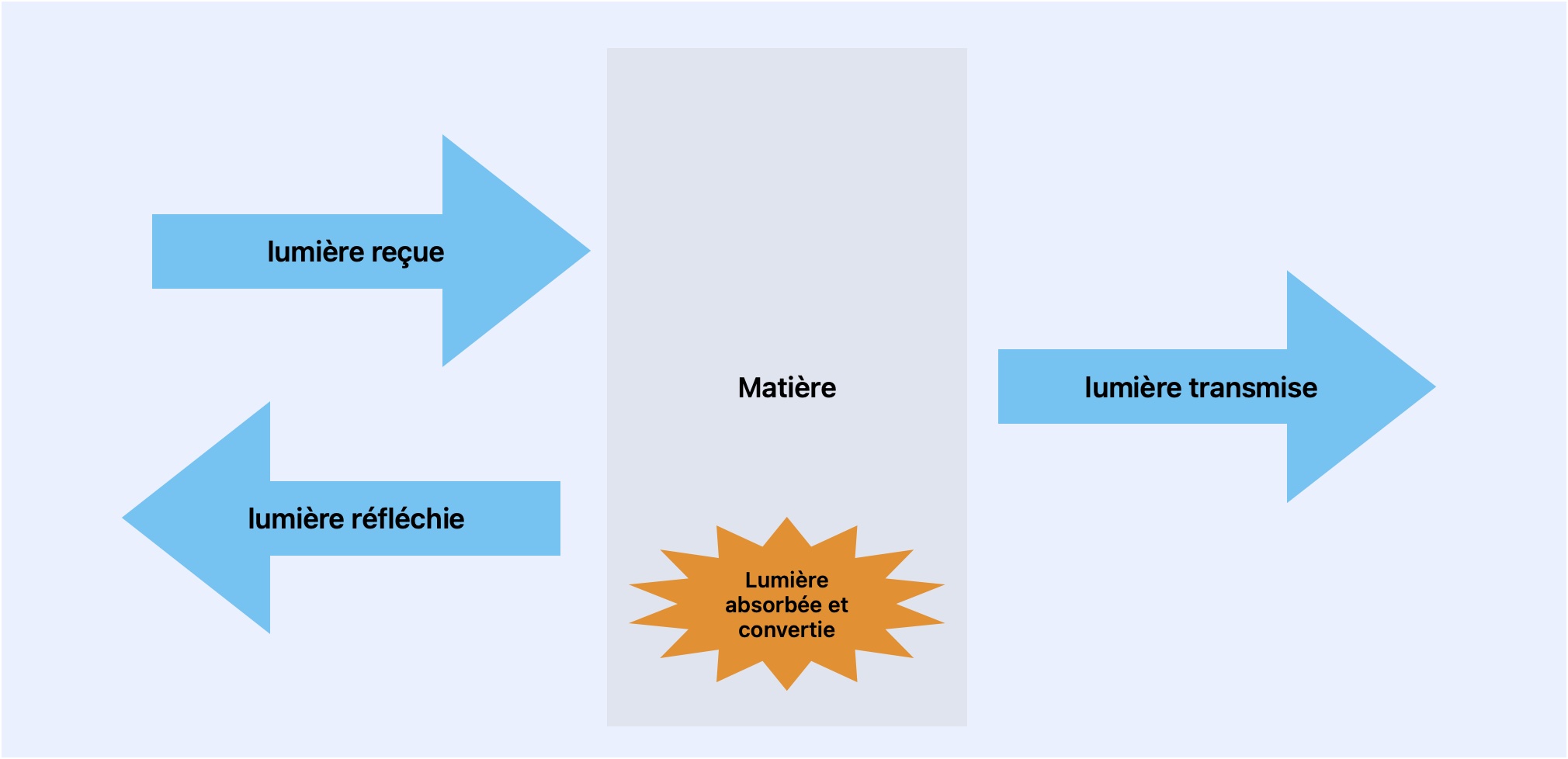
Exemples
Emission par un corps chaud
- Lorsque vous allumez un grille-pain vous pouvez observez de la lumière rouge à l'intérieur, c'est le métal qui émet cette lumière rouge en chauffant
- Les lampes à incandescence fonctionnent en faisant passer un courant électrique dans un fil de métal (tungstène) ce qui permet de chauffer ce fil jusqu'a 3000°C. On observe que le fil de métal chaud émet de la lumière
- Dans certains films ou séries comme Game of Thrones ou The Mandalorian on peut voir des forgerons qui comme au Moyen-Age font chauffer du métal pour réaliser des armes et des armures. Lorsque le métal est chaud on peut observer qu'il émet une lumière rouge.
- La lave c'est de la roche en fusion dont la température peut s'élever jusqu'à 1200°C elle émet une lumière rouge.
Interaction
- Le miroir parfait réfléchit toute la lumière qu'il reçoit il n'absorbe pas de lumière, il ne transmet pas de lumière.
- Les feuilles d'un arbre réfléchissent la lumière car on peut les observer en les éclairant mais elles en absorbent aussi une partie pour réaliser la photosynthèse (voir cours SVT).
- Le but du panneau solaire est d'absorber un maximum de la lumière du soleil pour la convertir sous forme d'énergie électrique.
- Un objet noir comme un pull ou une voiture absorbe complètement la lumière et la convertie en énergie thermique
- Le verre utilisé par exemple pour fabriquer des fenêtres, des objectifs d'appareil photo, ou des écrans, permet à la lumière d'être en majorité transmise. C'est pour cela que vous voyez l'extérieur lorsque vous regardez une fenêtre fermée.
2. Propagation
Où se propage la lumière ?
La lumière est capable de se propager dans tous les milieux transparents. Elle se propage différemment selon l'indice optique du milieu. L'indice optique :
Aussi appelé indice de réfraction, c'est un nombre supérieur ou égal 1 qui nous renseigne sur la vitesse
de propagation de la lumière dans le milieu.
On lui attribue la lettre \(n\) et on peut l'interpréter de la manière suivante :
- \(n = 1\) correspond au vide. La lumière se propage dans le vide à environ 300 000 kilomètres par seconde (\(300 \ 000 \ km.s^{-1}\))
- Plus \(n\) est grand plus la lumière est lente dans le milieu. Par exemple si \(n = 2\) cela signifie que la lumière va deux fois moins vite que dans le vide
A quelle vitesse se propage la lumière ?
La vitesse de la lumière dans le vide mentionnée précédemment est la vitesse maximale que vous rencontrerez. Aussi rapide soit l'objet auquel vous pensez, sa vitesse sera toujours inférieure à la vitesse de la lumière dans le vide.On attribue la lettre \(c\) à la vitesse de la lumière :
\(c \simeq 300 \ 000 \ km.s^{-1}\)
Dans un milieu matériel la vitesse varie en fonction de l'indice optique du milieu.
Comment se propage la lumière ?
La lumière se propage en ligne droite dans un milieu homogène mais change de comportement à l'interface entre deux milieux.A l'interface entre deux milieux transparents d'indice optique différents, une partie de la lumière est réfléchie dans le premier milieu d'où
vient la lumière, tandis qu'une autre partie traverse l'interface pour se propager dans le second milieu en modifiant sa direction de propagation,
on appelle ce phénomène la réfraction. Il faut bien différencier réflexion et réfraction
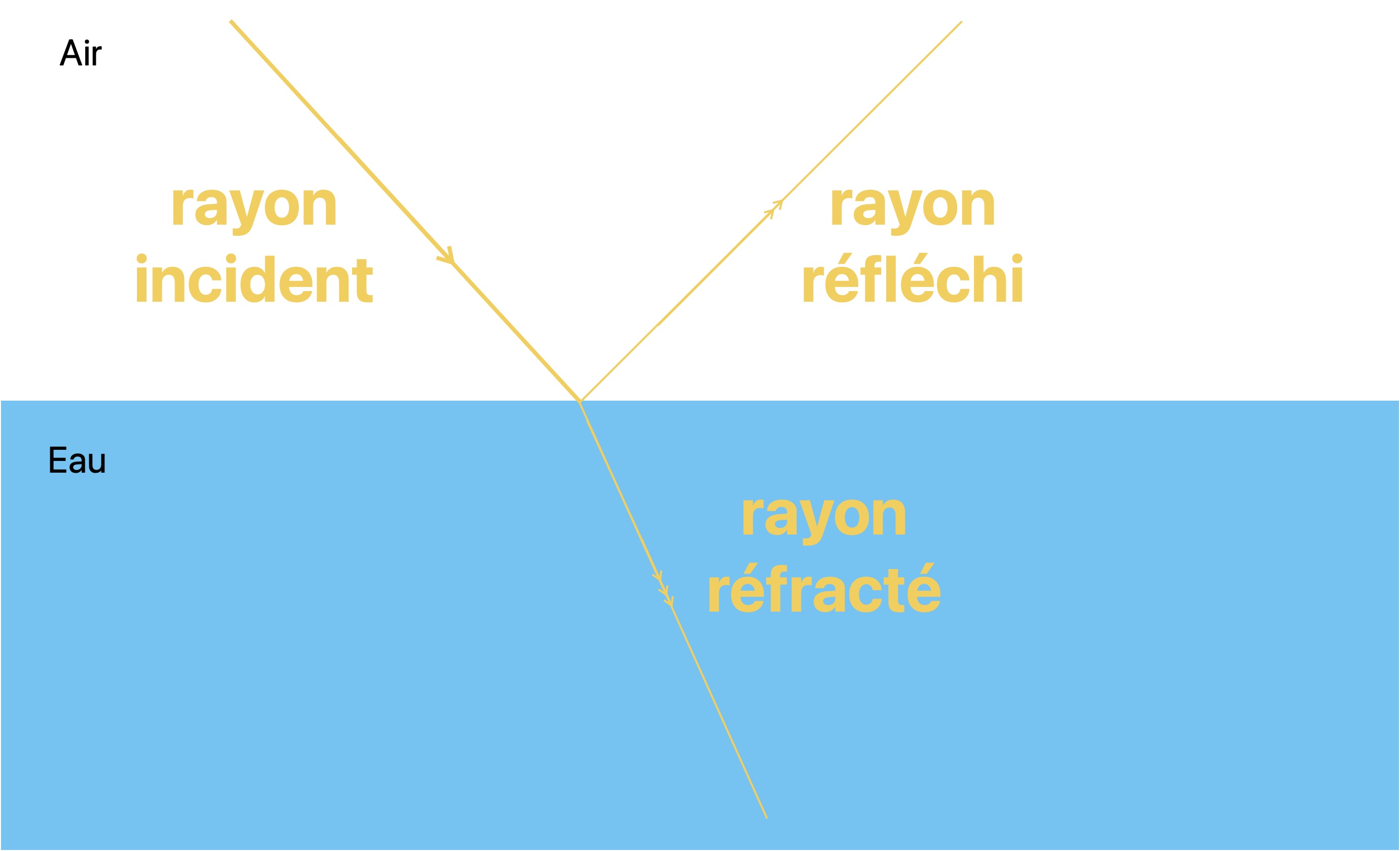
Lois de Snell-Descartes
Ces lois sont essentielles pour étudier la réflexion et la réfraction. Nous nous appuierons sur le schéma ci-dessous
pour les énoncer.
On appelle :
- \(i_1\) l'angle d'incidence
- \(r\) l'angle de réflexion
- \(i_2\) l'angle de réfraction
- \(n_1\) l'indice optique du milieu 1
- \(n_2\) l'indice optique du milieu 2
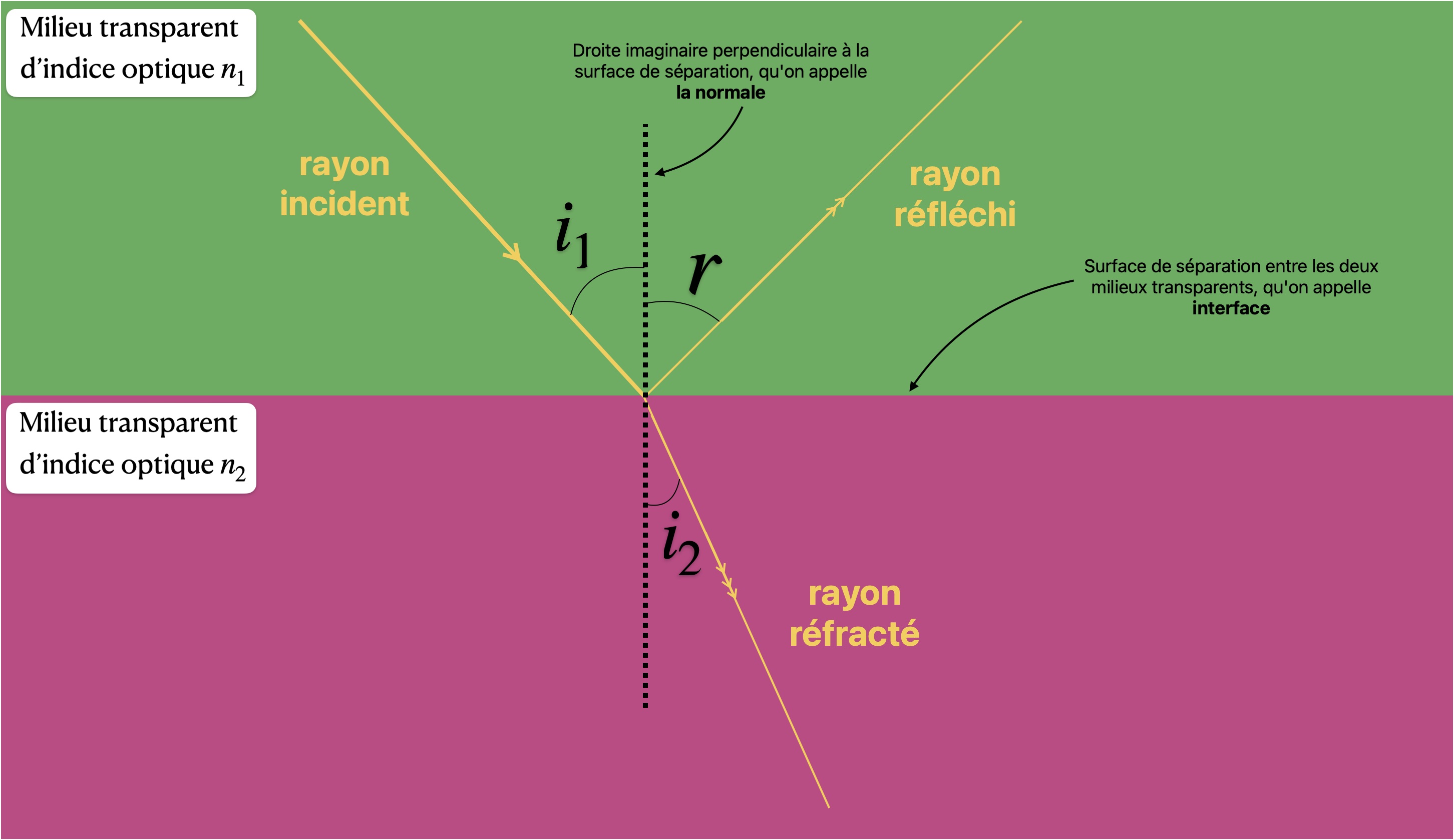
Loi de Snell-Descartes pour la réflexion :
- \(i_1 = r\)
- \(i_1\) et \(r\) sont contenus dans un même plan
Loi de Snell-Descartes pour la réfraction :
- \(n1 \cdot sin(i_1) =n2 \cdot sin(i_2) \)
- \(i_1\) et \(i_2\) sont contenus dans un même plan
Vocabulaire
Onde : perturbation qui se propage dans un milieu. Généralement sans déplacement de matière. Par exemple le son est une onde, la lumière aussi.Milieu : Support de la propagation d'une onde. Un milieu peut contenir de la matière (Un gaz, un liquide, un solide) on appelle ça un milieu matériel, ou ne pas contenir de matière, c'est ce qu'on appelle le vide.
Exemples
- \(n \simeq 1,0003\) dans l'air donc on peut considérer que la vitesse de la lumière est la même que dans le vide
- \(n \simeq 1,33\) dans l'eau donc la lumière est 1,33 fois plus lente dans l'eau que dans le vide
- \(n \simeq 1,5\) dans le verre donc la lumière est 1,5 fois plus lente dans le verre que dans le vide
- \(n \simeq 2,4\) dans le diamant donc la lumière est 2,4 fois plus lente dans le diamant que dans le vide
Analogie
Pour faire un trajet en voiture nous avons besoin :
- d'un support : La route
- de règles : Le code de la route
Pour que la lumière se propage elle a besoin :
- d'un support : Le milieu
- de règles :
- La propagation rectiligne dans un milieu homogène
- Les lois de Snell-Descartes
3. Former l'image d'un objet
Objet et Images
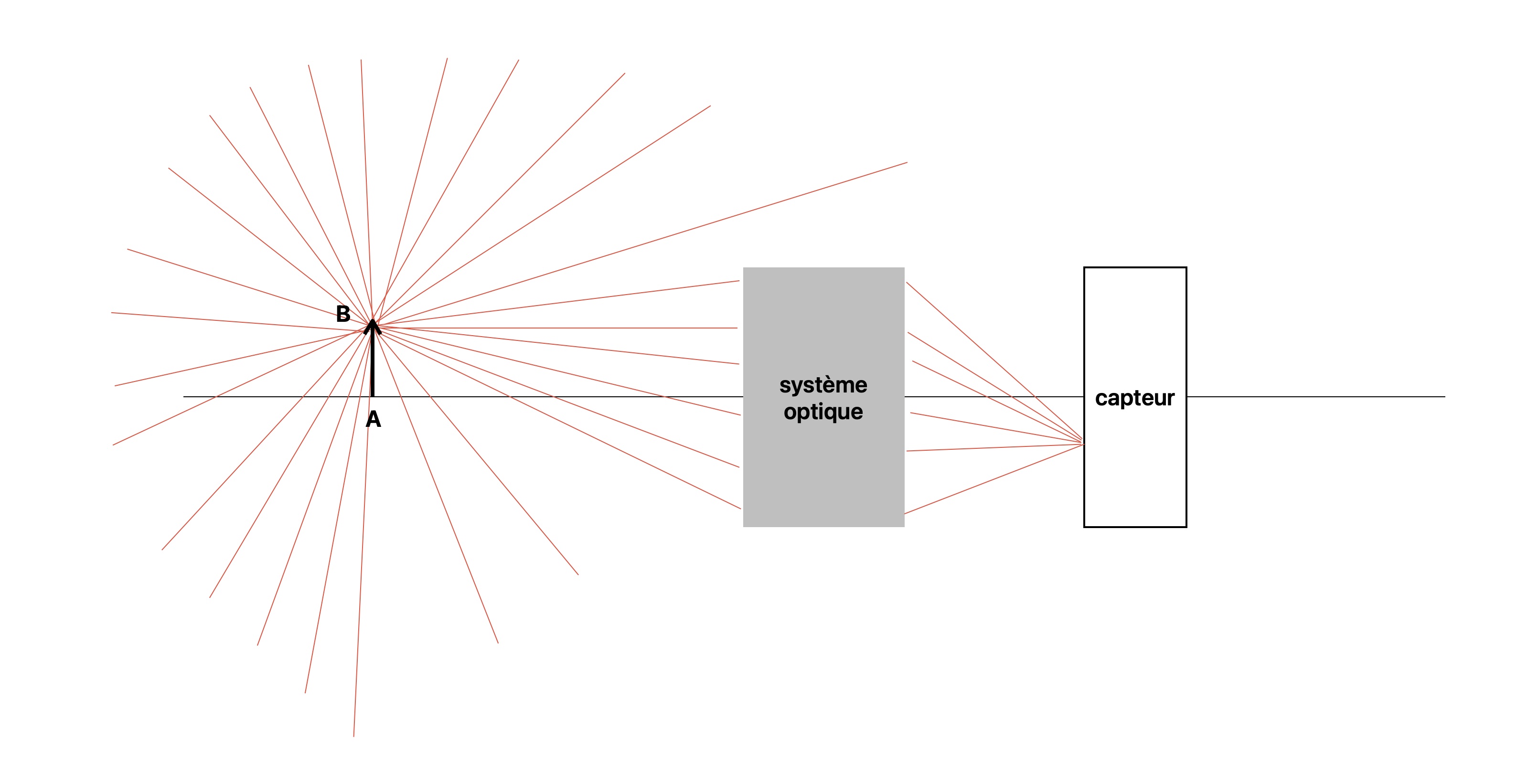
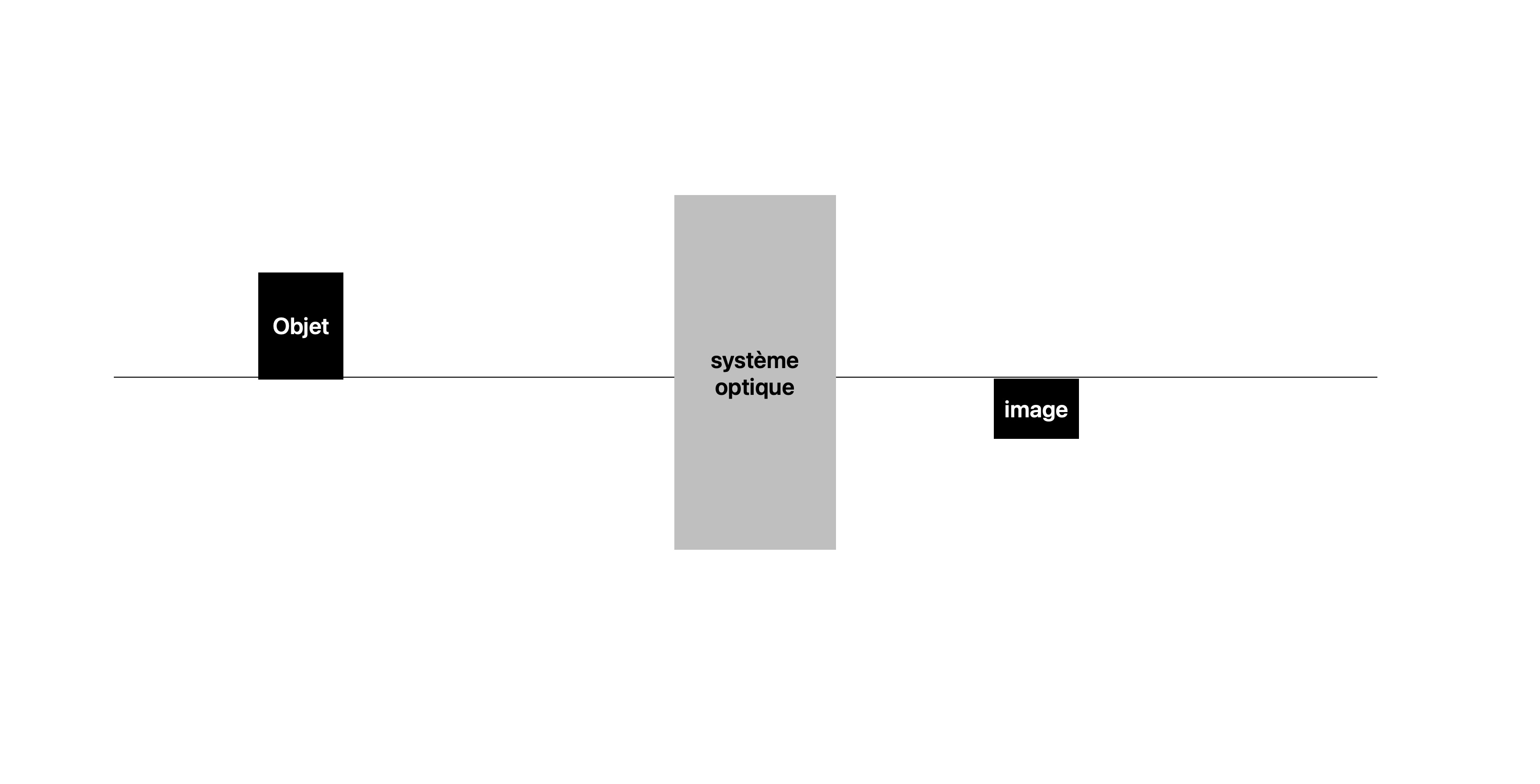
Un objet éclairé émet de la lumière dans toutes les directions, cette lumière peut être utilisée pour former l'image de l'objet. Par exemple l'oeil est capable de former l'image d'un objet dont il reçoit la lumière. La différence entre objet et image c'est que l'objet est constitué de matière alors que l'image n'est pas constitué de matière. L'image est formée a partir des rayons lumineux émis par un objet.Système optique et capteur
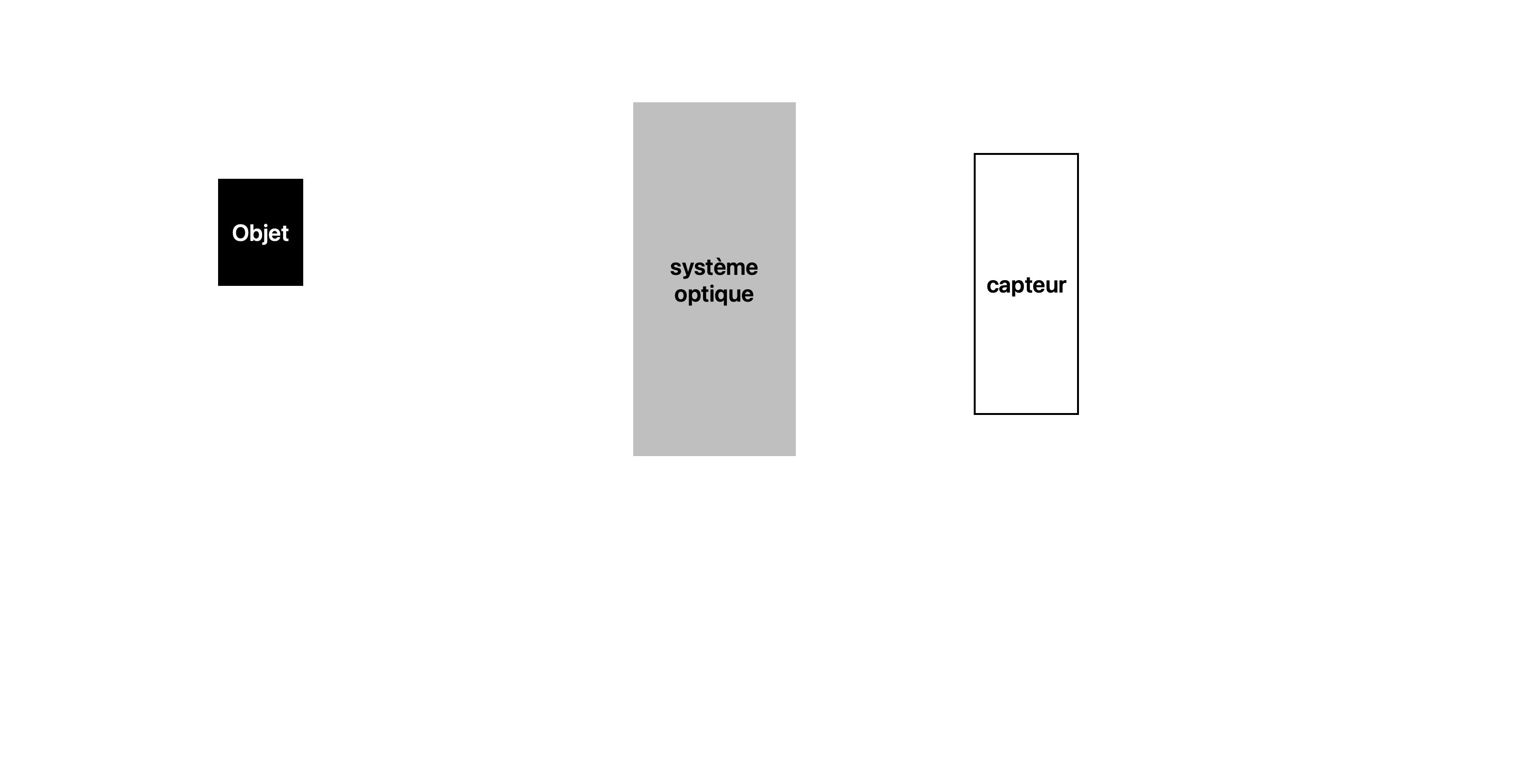
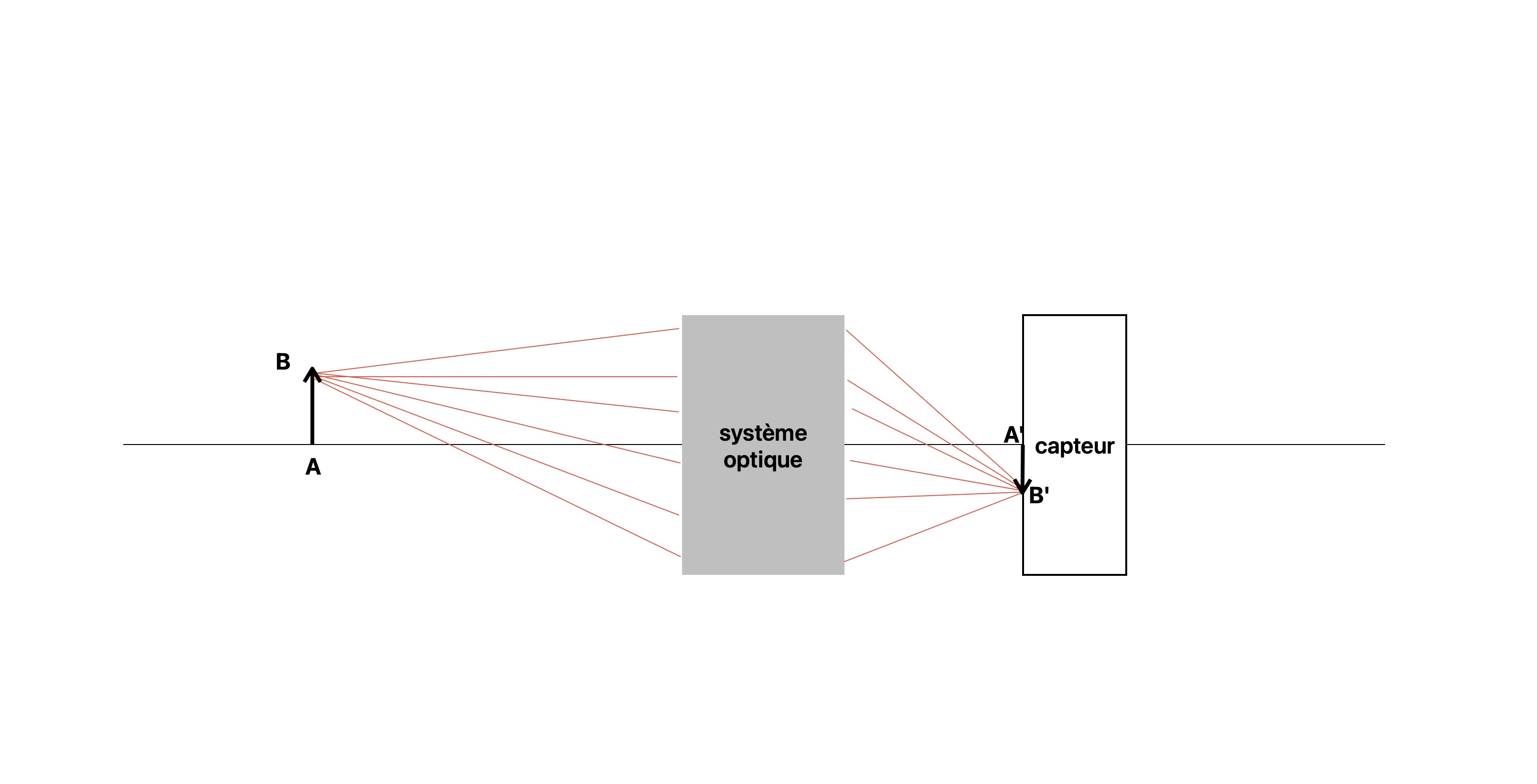
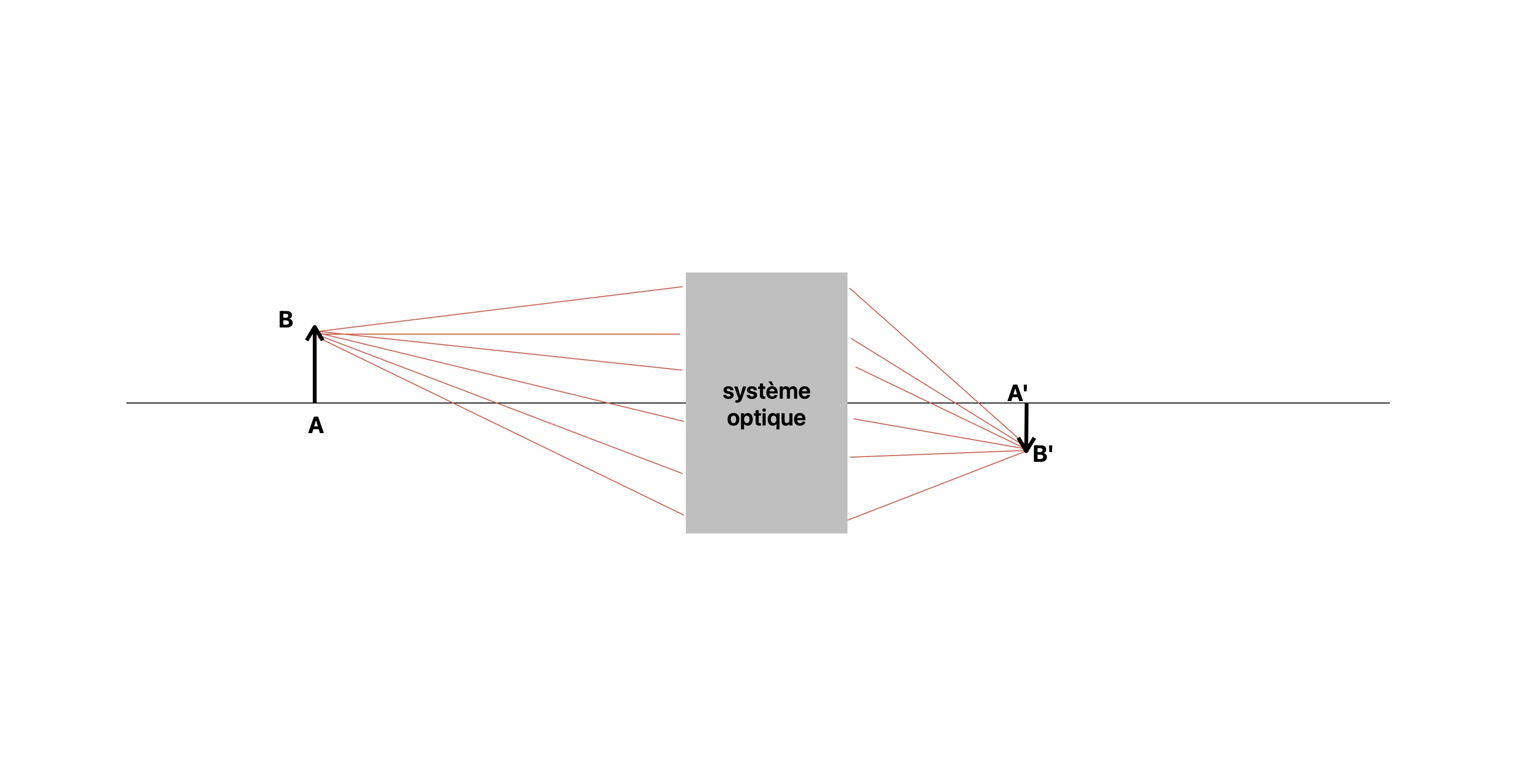
La plupart des appareils capables de former l'image d'un objet sont constitués d'un système optique et d'un capteur. Le système optique forme l'image d'un objet sur le capteur.La schématisation
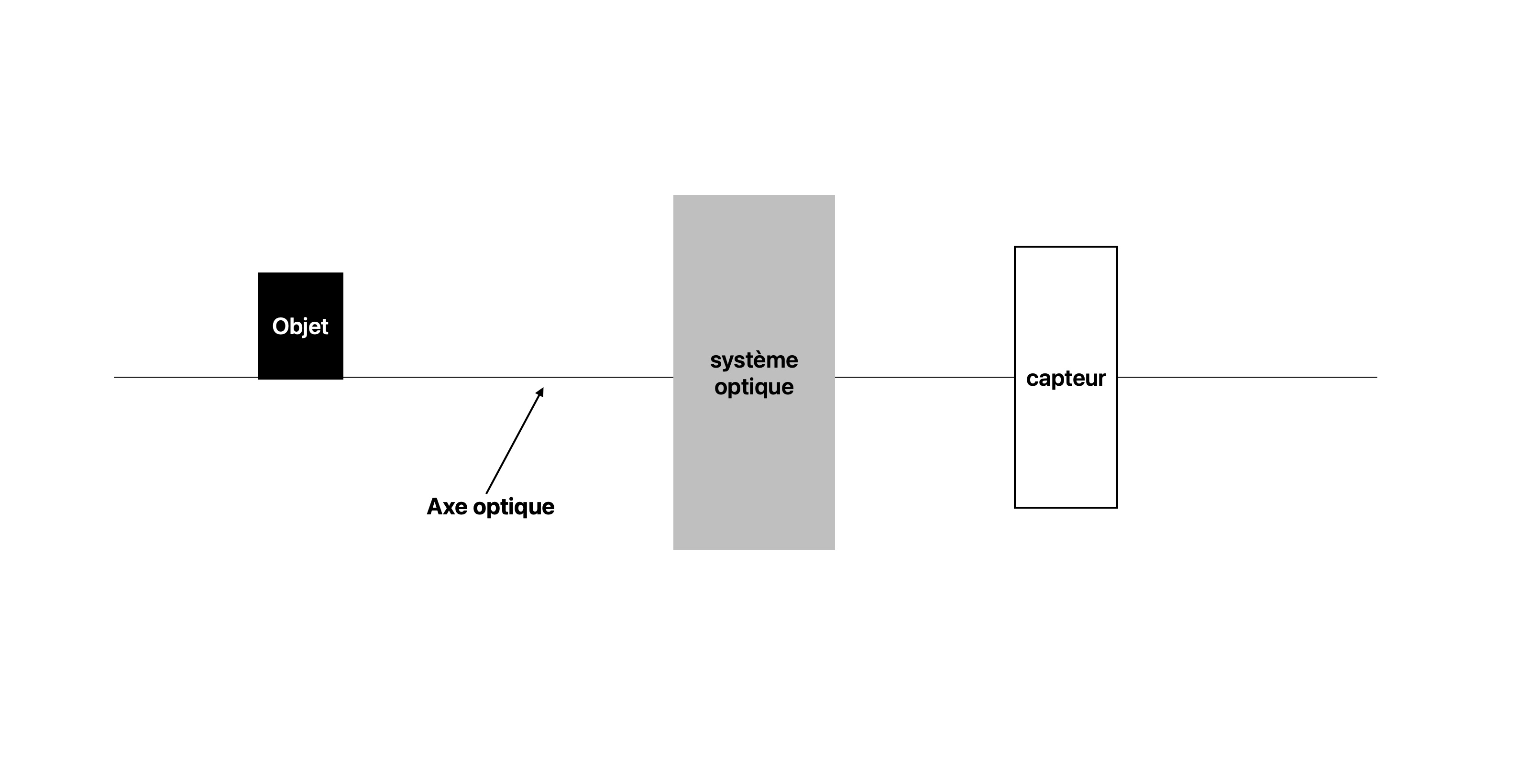
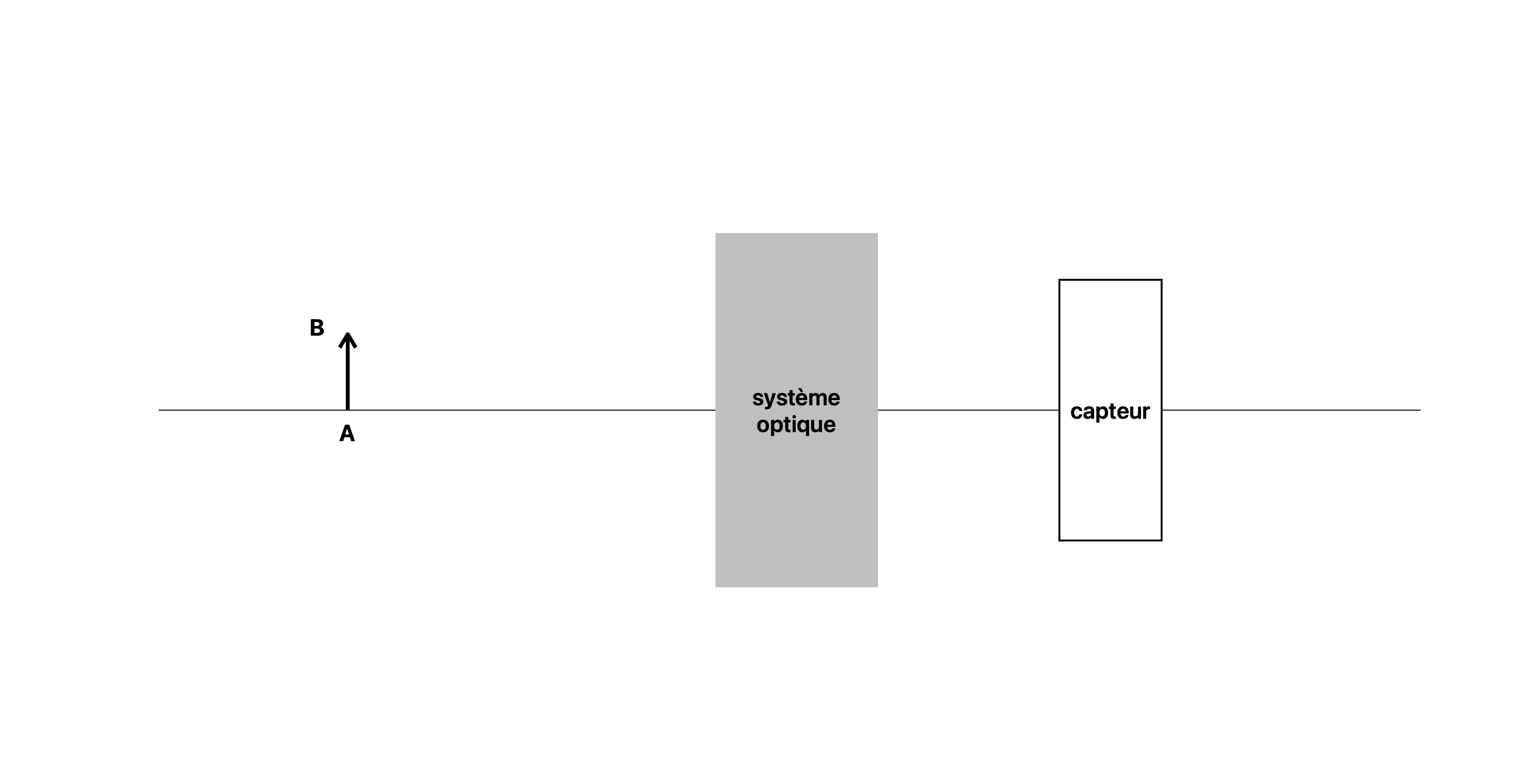
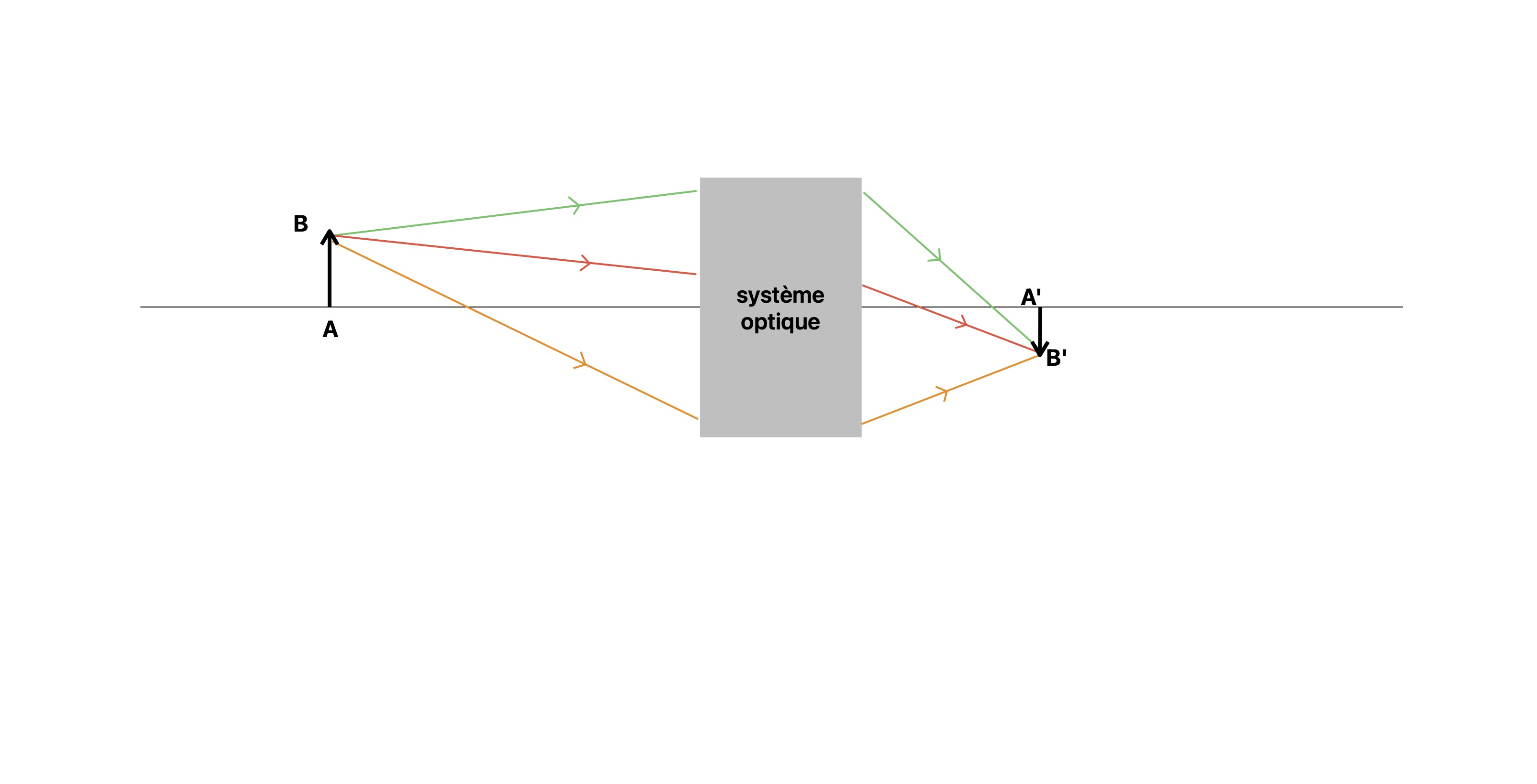
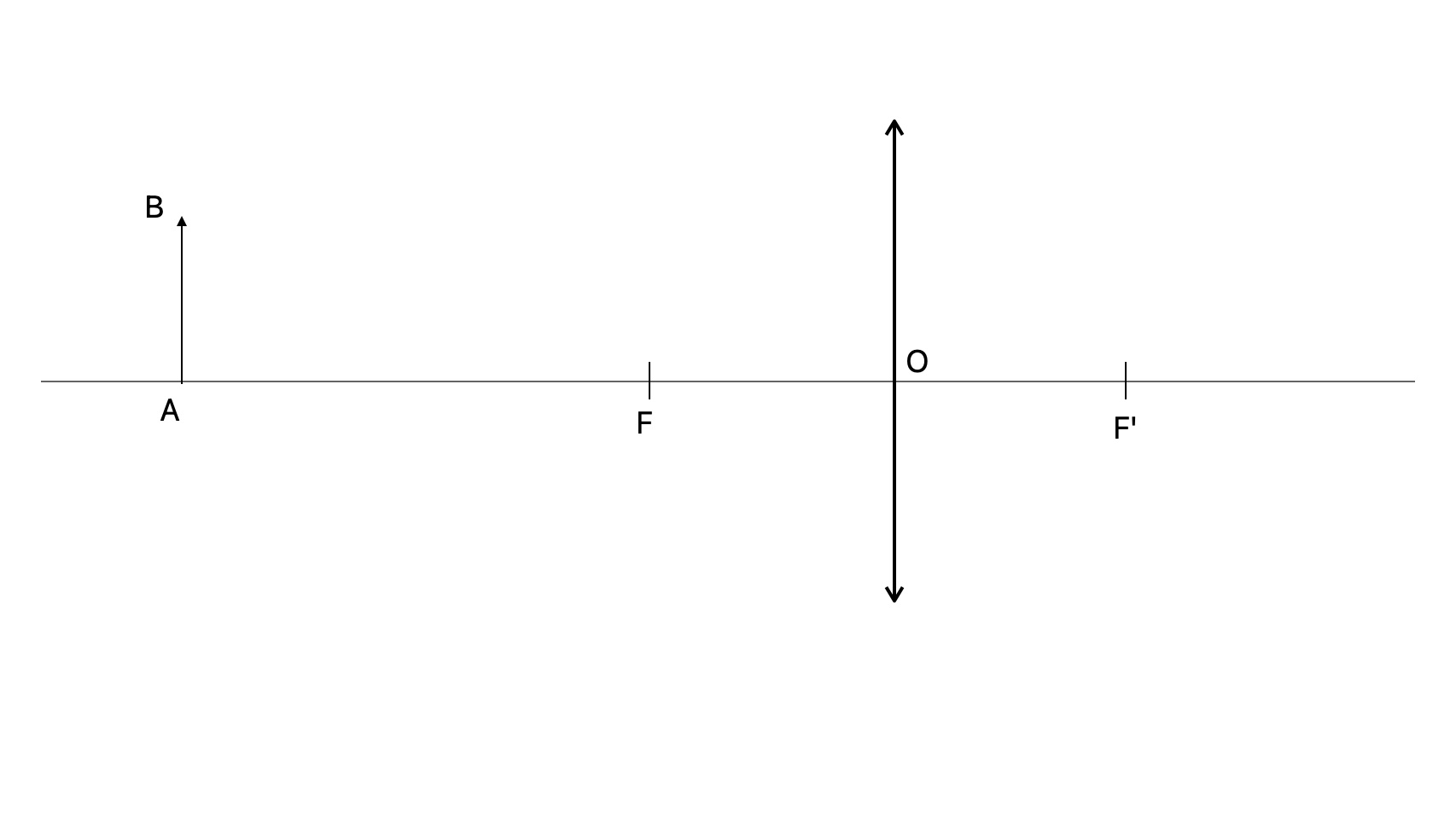
Le schéma de la formation d'une image par un système optique ressemble à la figure ci dessous.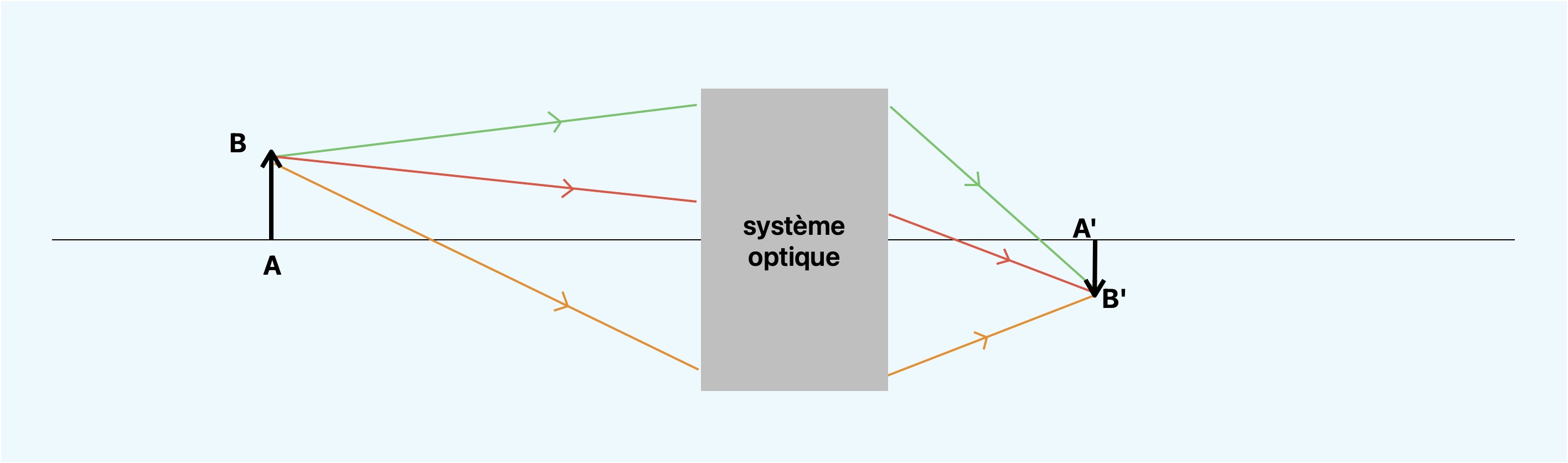
Comment interpréter et construire ce schéma
Eléments de base
On représente l'objet, le système optique et le capteur alignés.
Axe optique
L'axe optique est une droite qui passe par le centre du système optique. On s'en servira de repère pour tracer les rayons lumineux.
Simplification : représenter un objet
E général tous les points d'un objets émettent une infinité de rayons lumineux dans toutes les directions, ce qui serait très pénible à dessiner. On va donc se contenter de représenter l'objet par une flèche de même hauteur reliant les points A et B.
Besoin de simplifier
Comme indiqué précédemment le point B qui appartient à l'objet émet une infinité de rayons lumineux. Nous pourrions essayer de tous les représenter mais comme le montre le schéma ci-dessus, ce serait encore une fois très pénible.
Simplification : Tracer les rayons lumineux
On ne représentera que certains rayons qui passent par le système optique. Ces rayons sortent du système optique et forment l'image du point B sur le capteur. L'image du point B est aussi un point qu'on appelle B' (prononcé "B prime"). On peut aussi représenter A' en traçant une flèche qui part de l'axe optique.
Le capteur
Généralement on ne représente pas le capteur et on se contente de schématiser l'image par une flèche, de la même manière que l'objet.
Schéma final
En réalité puisque tous les rayons vont au même endroit, il suffit de tracer au moins 2 rayons pour savoir ou se forme l'image. Ici 3 rayons sont représentés d'une couleur différente pour pouvoir différencier le chemin de chacun. Une petite flèche permet d'indiquer le sens de propagation de la lumière.
Conclusion
Grâce au schéma précédent on sait donc où est l'image de l'objet formée par le système optique
Un système optique simple : La lentille mince convergente
Cet outil va nous permettre de former l'image d'objets en séance de travaux pratiques. Il est utilisé pour modéliser certains télescope, les microscopes, ou encore des lunettes de vue.
Une lentille mince convergente est un objet transparent généralement en verre. Sa géométrie permet de changer
la direction des rayons lumineux qu'elle reçoit.
Tamasflex, CC BY-SA 3.0, via Wikimedia Commons
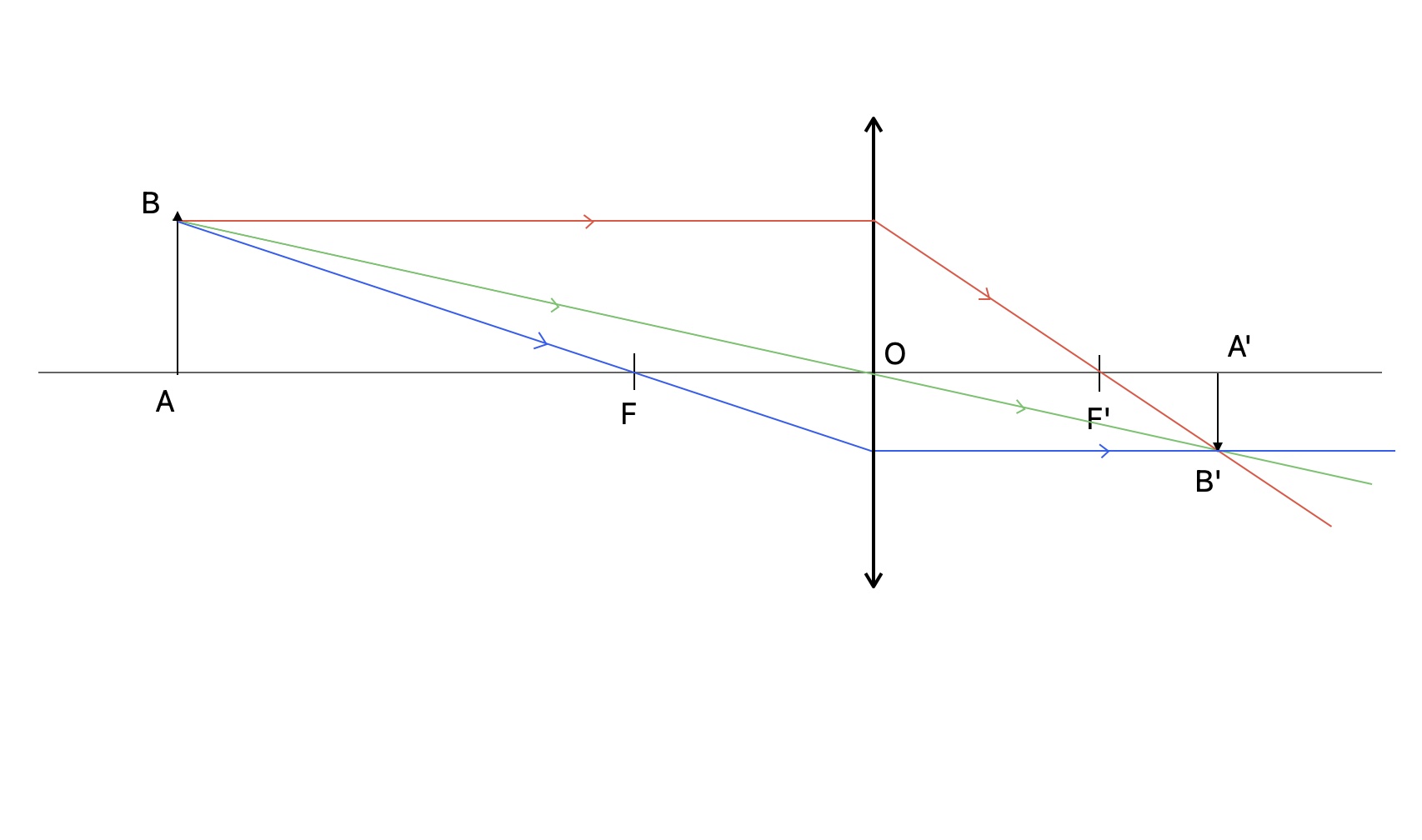
Sur un schéma d'optique on la représente par un segment fléché à chaque extrémité. Plusieurs points sont importants,
on appelle :
- O : Le centre de la lentille mince convergente, c'est le point d'intersection entre la lentille et l'axe optique. Tout rayon lumineux passant par ce point n'est pas dévié.
- F : Le foyer objet de la lentille, tout rayon lumineux passant par ce point ressort de la lentille parallèle a l'axe optique
- F' : Le foyer image, tout rayon lumineux parallèle à l'axe optique ressort de la lentille en passant par ce point
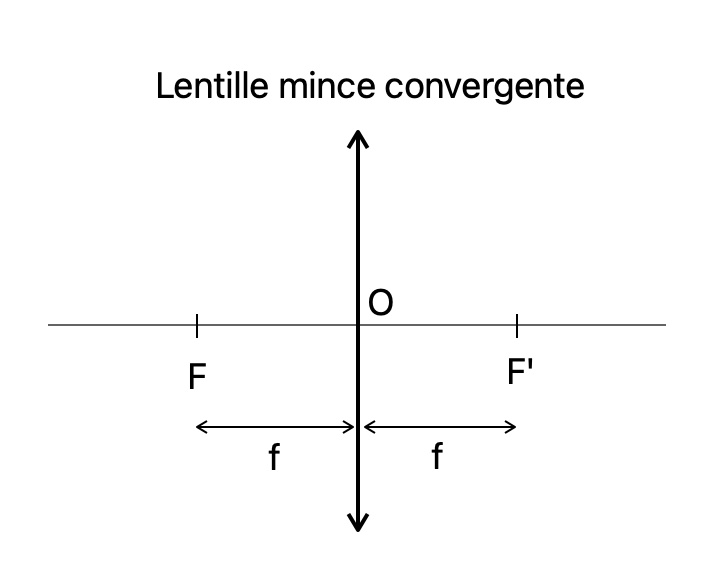
La distance focale
\(OF = OF' = f \) et on appelle \(f\) la distance focale de la lentille. Sa valeur peut être différente en fonction de la lentille.Méthode : Former l'image d'un objet avec une lentille
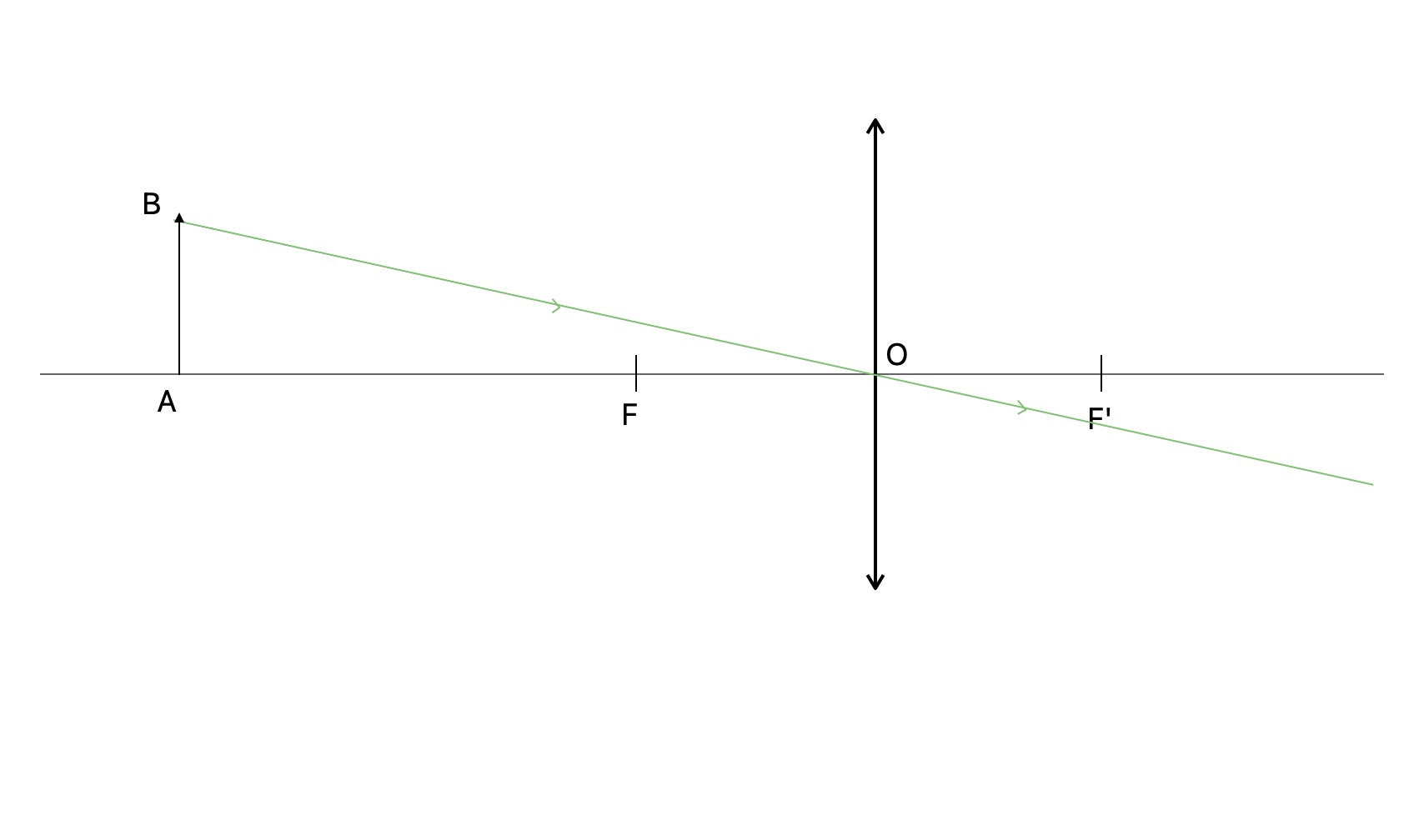
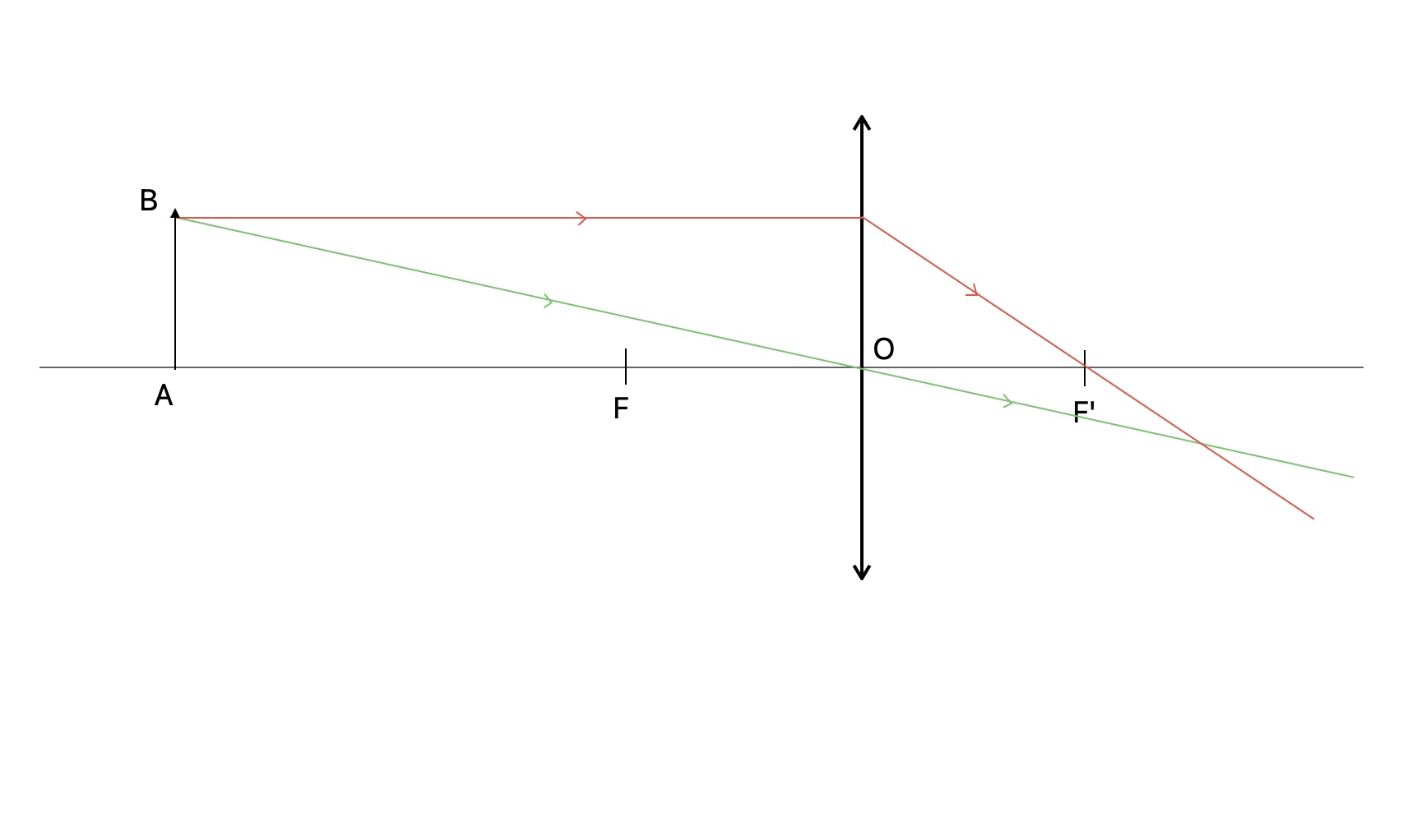
Trois règles déjà énoncées sont à respecter :- Le rayon passant par O n'est pas dévié
- Le rayon parallèle à l'axe optique sort en passant par F'
- Le rayon passant par F sort parallèle à l'axe optique
Situation initiale
On aligne l'objet AB et la lentille
Premier rayon
On peut toujours tracer le rayon passant par O qui n'est pas dévié
Foyer image
Traçer le rayon parallèle à l'axe optique qui sortira de la lentille en passant par le foyer image F'
Former l'image
L'image du point B se forme la ou les rayons se croisent pour former le point B'. On peut donc savoir ou sera l'image A' de A en traçant la flèche qui relie B' à l'axe optique. A'B' est l'image de AB.
Foyer objet
On peut vérifier que tous les rayons émis par B se rejoignent en B' en traçant le dernier rayon qui passe par le foyer objet F et ressort parallèle à l'axe optique.
4. La notion de grandissement
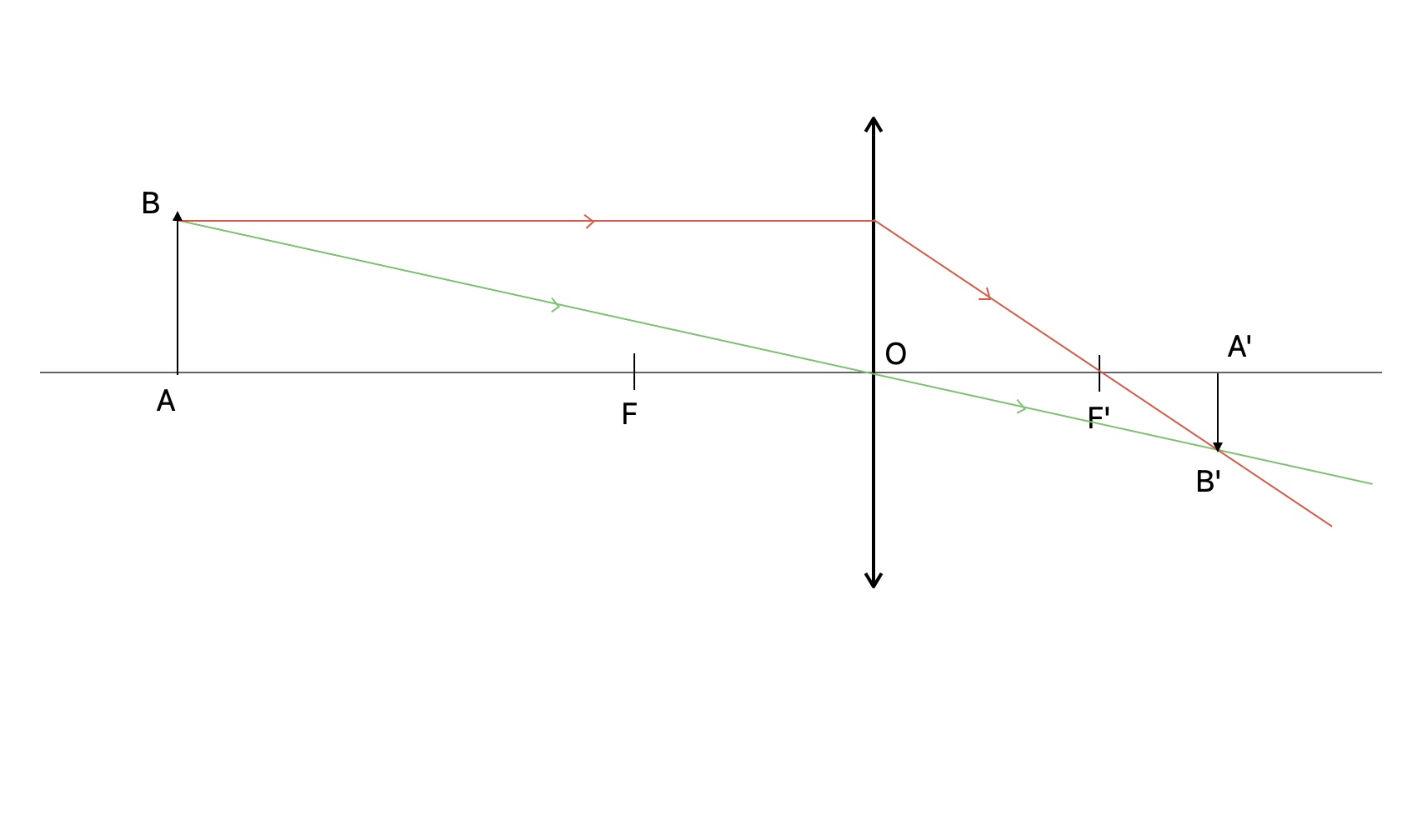
Comme on peut le constater sur les schémas précédents la taille de l'image n'est pas la même que celle de l'objet. On observe également que l'image peut être vers le bas on dit que l'image est renversée.
Le Grandissement
On appelle grandissement le rapport entre la taille de l'image A'B' et la taille de l'objet AB. On le note \(\gamma \) ("gamma") et pour avoir sa valeur absolue on utilise la formule suivante : \( | \gamma | = \frac{A'B'}{AB} \)
avec |\(\gamma\)| la valeur absolue de \(\gamma\), \(A'B'\) la longueur de l'image et \(AB\),
la longueur de l'objet.
Pour trouver le signe du grandissement il faut regarder si l'image est renversée.
- Si l'image est renversée le grandissement est négatif : \(\gamma < 0\)
- Si l'image n'est pas renversée le grandissement est positif : \(\gamma > 0\)
Exemple
- Si \(\gamma = 0,5\) cela veut dire que l'image est deux fois plus petite que l'objet et qu'elle n'est pas renversée.
- Si \(\gamma = - 1\) cela veut dire que l'image fait la même taille que l'objet et qu'elle est renversée.
- Si \(\gamma = - 2\) cela veut dire que l'image est 2 fois plus grande que l'objet et qu'elle est renversée.
5. Couleur et longueur d'onde
C'est quoi une couleur ?
Chaque couleur qu'on perçoit est associée à ce qu'on appelle une longueur d'onde. Cette longueur d'onde est notée \(\lambda\) est elle s'exprime la plupart du temps en nanomètre (\(1 \ \text{nm} = 10^{-9} \ \text{m}\)). Sur le logiciel ci-dessous proposé par academo.org vous pouvez constater visuellement la correspondance entre longueur d'onde et couleur.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
Analogie avec le son
Lorsqu'on a étudié le son on a vu que l'oreille humaine entendait les fréquences allant généralement de 20Hz a 20kHz. L'oeil humain est également limité, il peut voir les longueurs d'onde allant généralement de 400nm à 800nm.Retenez que les longueurs d'onde visibles qu'on peut associer à une couleur vont de 400nm à 800nm. Les longueurs d'onde juste en dessous de 400nm sont associées au rayonnement ultraviolet
tandis que les longueurs d'ondes juste au dessus de 800nm sont associées au rayonnement infrarouge.
6. Monochromatique et Polychromatique
Rayonnement monochromatique
Monochromatique est constitué du préfixe "mono" (unique) suivi de "chromatique" (couleur). On parle de rayonnement monochromatique lorsque la lumière émise ne contient qu'une seule longueur d'ondeRayonnement polychromatique
Polychromatique est constitué du préfixe "poly" (plusieurs) suivi de "chromatique" (couleur). On parle de rayonnement polychromatique lorsque la lumière émise contient plusieurs longueurs d'ondesAnalogie avec le son
Lorsqu'on a étudié le son on a vu qu'on pouvait émettre un son qui ne contient qu'une seule fréquence à l'aide d'un diapason. En revanche si on écoute un orchestre, le son perçu sera beaucoup plus riche en fréquence car tous les musiciens ne jouerons pas tous la même note et pas tous avec le même instrument. On peut avoir le même raisonnement avec la lumière. On peut émettre un rayonnement monochromatique à l'aide d'un laser. En revanche la plupart des sources lumineuses contiennent plusieurs longueurs d'onde et notamment les sources de lumière blanche qui émettent toutes les longueurs d'ondes visibles comme on peut le constater grâce a la dispersion par un prisme.7. Dispersion de la lumière par un prisme
Description
Lorsqu'on émet un rayon de lumière blanche sur un prisme, on observe à la sortie du prisme toutes les couleurs visibles à l'oeil nu.Explication
La lumière blanche est un rayonnement polychromatique composée de toutes les longueurs d'ondes visibles à l'oeil nu. Le prisme est un élément dispersif capable de séparer et révéler les différentes longueurs d'ondes contenu dans un rayon lumineux.8. Les spectres d'émission
La notion de spectre d'emission
Le spectre d'émission indique toute les longueurs d'ondes qui composent le rayonnement d'une source de lumière.Exemples
Le spectre émis par un corps chaud
C'est un spectre continu qui dépend de la température du corps. Plus il est chaud plus il contient de longueur d'onde visibles. L'echelle gradué correspond
à la valeur de la longueur d'onde en nanomètre. Lorsqu'on fait chauffer progressivement le filament dans une ampoule il commence par émettre de la lumière orange
pour progressivement émettre de la lumière blanche qui contient toutes les longueurs d'ondes visibles.
Le spectre émis par un laser
Les laser émettent un rayonnement quasi monochromatique. Ici nous prenons l'exemple d'un laser rouge dont le spectre présente une seule raie de longueur d'onde
associée à la couleur rouge.
Spectre de raie d'un gaz
Certaines lampes qu'on appelle "lampes à vapeur" fonctionnent suivant ce principe : Lorsqu'on chauffe un gaz à basse pression, il émet de la lumière.
Le spectre de la lumière émise s'appelle spectre de raies et permet d'identifier le gaz présent dans la lampe.
Spectre d'une lampe à vapeur d'Hydrogène :
